[A] $\dfrac{2u+v}{v-u}$.
[B] $\dfrac{2uv}{v-u}$.
[C] $\dfrac{uv}{v-u}$.
[D] $\dfrac{2(u+v)}{v-u}$.
Solução
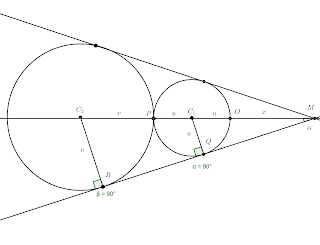
Traçando segmentos $(C_{2}R$ e $C_{1}Q)$ de medidas $v$ e $u$, respectivamente, nos pontos de tangencia, formam-se ângulos de $90^{\circ}$. Os segmentos $MO, \, OC_{1}, \, C_{1}P$ e $PC_{2}$ têm medidas iguais a $x, \, u, \, u$ e $v$, respectivamente. Nota-se dois triângulos retângulos, $MQC_{1}$ e $MRC_{2}$, com um ângulo $\alpha$ no ponto $M$. A figura descrita é representada da seguinte maneira:
Desta forma, desenvolve-se algumas relações trigonométricas nos triângulos: $\vartriangle MQC_{1}$: $$\textrm{sen}\,\alpha=\dfrac{\textrm{cateto oposto}}{\textrm{hipotenusa}}$$ $$\textrm{sen}\,\alpha=\dfrac{u}{x+u}$$ $\vartriangle MRC_{2}$: $$\textrm{sen}\,\alpha=\dfrac{\textrm{cateto oposto}}{\textrm{hipotenusa}}$$ $$\textrm{sen}\,\alpha=\dfrac{v}{x+2u+v}$$ Igualando $\textrm{sen}\,\alpha$: $$\dfrac{u}{x+u}=\dfrac{v}{x+2u+v}$$ $$vx+uv=ux+2u^{2}+uv$$ $$vx-x=2u^{2}$$ $$x(v-u)=2u^{2}$$ $$x=\dfrac{2u^{2}}{v-u}$$ Como $MP=x+2u$: $$MP=\dfrac{2u^{2}}{v-u}+2u=\dfrac{2u^{2}+2uv-2u^{2}}{v-u}=\dfrac{2uv}{v-u}$$
Resposta: Item B